ТЕОРИЯ И
КЛАССИФИКАЦИЯ
Главная страница
ВОЛНОВЫЕ И КВАЗИСТАЦИОНАРНЫЕ спироны НОСИТЕЛЕЙ ЗАРЯДА
wave and quasi-stationary spirons of charge charrier
Из уравнения спиронных волн следует, что в частном случае, когда отсутствует классическая компонента спиронной волны, может существовать ее замкнутая нелинейная спирально-вихревая компонента, представляющая собой пространственно локализованный объект, образованный движущимися носителями зарядов. Эти локальные объекты названы спиронами носителей заряда. Из уравнения спиронных волн носителей заряда следует, что спироны носителей заряда могут быть двух типов: волновые и квазистационарные. Уравнение волновых спиронов носителей заряда имеет форму аналогичную уравнению Клейна-Гордона и допускает квантованные решения. Уравнение квазистационарных спиронов носителей заряда имеет форму аналогичную уравнению Гельмгольца и также допускает квантованные решения. Оба уравнения спиронов являются принципиально нелинейными независимо от линейности среды. Открытие нелинейных спиронов носителей заряда объясняет существование шаровых и четочных молний, искусственных долгоживущих плазменных образований, Z-пинчей, устойчивость атомов.
Спиричев Ю.А.
Spirichev Yu.A.
E-mail: SPIRON@sura.ru
Дата 10.01.2003г.
Научно-информационный центр
спирально-вихревых процессов
и явлений "СПИРОН"
Существует ряд таких явлений, как шаровые и четочные молнии, искусственные долгоживущие плазменные образования, Z-пинчи, грануляция солнечной фотосферы, многочисленные виды самоорганзации и упорядочения среды с образованием устойчивых пространственно локализованных объектов. Для объяснения этих явлений отсутствуют однозначные, взаимосвязанные физические теории и природа их образования не всегда ясна. Решающую роль в процессах самоорганизации среды играют спиронные волны носителей заряда. В работе [1] приведено нелинейное волновое уравнение движения носителей заряда, описывающее их спиронные волны:
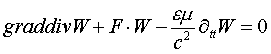 (1)
(1)
Здесь F нелинейная скалярная функция от скорости W и ее производных первого порядка по времени и пространству:
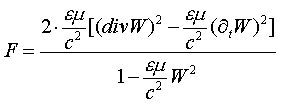
Нелинейные спиронные волны, описываемые уравнением (1) можно представить в виде суперпозиции двух компонент:
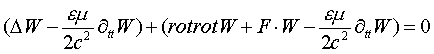 (2)
(2)
Первая, классическая компонента в общем случае описывает сферическую волну, радиально распространяющуюся из центра возбуждения и подчиняющуюся волновому уравнению Даламбера, а вторая компонента представляет собой замкнутую нелинейную спирально-вихревую волну. Кинематическое уравнение (1) по своей структуре аналогично уравнению Клейна-Гордона, но имеет от него два отличия. Во-первых, отличается видом своей «пространственной» частной производной второго порядка. В уравнении Клейна-Гордона эта производная, как и в классическом уравнении Даламбера, представляет собой лапласиан, а в уравнении (1) - это градиент дивергенции. Вторым отличием является то, что в уравнении Клейна-Гордона коэффициент F при W является константой, а в уравнении (1) он представляет собой нелинейную скалярную функцию от W и производных первого порядка от W по пространству и времени. Из уравнения спиронных волн записанного в виде уравнения (2) для двух компонент волны можно сделать вывод, что для частного случая равенства нулю выражения, описывающего классическую волновую компоненту
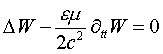
в природе может самостоятельно существовать, её вторая компонента в виде замкнутых спирально-вихревых нелинейных волн, в уравнении которых «пространственная» частная производная второго порядка представляет собой ротор от ротора вектора W
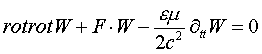 (3)
(3)
В соответствии с теоремой Стокса [2], поток ротора вектора через поверхность равен его циркуляции по замкнутому контуру, на который опирается эта поверхность. Так как векторы rotJ и rotrotJ взаимно ортогональны, то “пространственная” часть второй компоненты волны, описываемой ротором от ротора вектора W, определяет циркуляцию этого вектора по замкнутому спиральному контуру и описывает замкнутую спирально-вихревую волну вектора W. Уравнение (3) по своей структуре аналогично уравнению Клейна-Гордона имеющего дискретные (квантованные) решения, а так как замкнутые волны, описываемые уравнением (3) не распространяются в пространстве, то они являются локализованными в пространстве волновыми квантованными объектами. В соответствии с классификацией приведенной в работе [3], объекты, описываемые уравнением (3) относятся к классу волновых спиронов носителей заряда. Уравнение (1) можно записать в виде
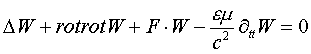 (4)
(4)
Из уравнения (4) для частного случая – отсутствия классической волновой части
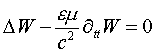
следует возможность существования в природе замкнутых периодических нелинейных квазистационарных спирально-вихревых структур описываемых нелинейным уравнением
![]() (5)
(5)
Под квазистационарностью этих структур, в отличии от волновых, понимается отсутствие в уравнении (5) производной второго порядка по времени. В соответствии с классификацией приведенной в работе [3] объекты, описываемые уравнением (5), относятся к классу нелинейных квазистационарных спиронов носителей заряда. Кинематическое уравнение (5) по своей структуре, аналогично уравнению Гельмгольца, но имеет от него два отличия. Во-первых, отличается своей «пространственной» частной производной второго порядка. В уравнении Гельмгольца эта производная, как и в классическом уравнении Даламбера, представляет собой лапласиан, а в уравнении (5), это ротор от ротора. Вторым отличием является то, что в уравнении Гельмгольца коэффициент F при W является константой, а в уравнении (5) он представляет собой нелинейную скалярную функцию от W и производных первого порядка от W по пространству и времени. Так как уравнение Гельмгольца может иметь дискретные (квантованные) решения в виде стоячих волн, то и уравнение (5) будет иметь дискретные (квантованные) решения на замкнутом спиральном контуре в виде стоячих волн и описывать замкнутые нелинейные квантованные спирально-вихревые структуры. Таким образом, на основании кинематических уравнений (3) и (5) можно сделать вывод о возможности существования в природе самосогласованных замкнутых периодических нелинейных волновых и квазистационарных квантованных спирально-вихревых структур - спиронов, образованных носителями заряда в результате их взаимодействия с самосогласованным электромагнитным полем и возникающих из нелинейных спиронных волн носителей заряда. Существует большое количество явлений, в которых подтверждается факт существования в природе спиронов носителей заряда. Это многообразие связано с тем, что спироны возникают при коллективном, самосогласованном движении носителей заряда, из которых состоит материальная среда нашего мира, следовательно, спироны могут возникать в любой материальной среде, будь то твердое вещество, жидкость или космическая плазма. Одним из самых ярких примеров образования спиронов служит четочная молния. Термином четочная молния обозначают последовательность светящихся устойчивых и относительно небольших сферических образований наблюдаемых в атмосфере и остающихся от канала прохождения обычной линейной молнии. Считается, что четочная молния возникает на месте канала обычной молнии испытывающего периодические продольные колебания интенсивности вследствие возмущения. Такой канал затухает и превращается в серию почти равномерных распределённых областей с устойчивым свечением [4]. Ее характер в виде периодической структуры канала линейной молнии, совершенно однозначно говорит, что причиной такой периодичности является волновой процесс, возникший в канале линейной молнии. Из уравнения (1) следует, что в плазменной среде может возбуждаться спиронная волна, а так как размеры плазменной среды определяются размерами разрядного канала молнии, то возникшая спирально-вихревая волна также ограничена размерами разрядного канала. При этом классическая компонента может существовать только в одномерном виде (вдоль канала молнии) и по этому в соответствии с уравнением (2) в разрядном канале остается только замкнутая компонента спирально-вихревой волны, которая может существовать в замкнутом объеме. При этом канал линейной молнии разделяется на замкнутые относительно долгоживущие спирально-вихревые волновые структуры. Аналогичные процессы зарегистрированы в лабораторных условиях при высоковольтных разрядах напряжением 2х107 В и энергией 12 Дж в импульсе, во время которых зарегистрирована четочная структура остатка канала разряда [4]. Явления аналогичные четочной молнии наблюдаются в лабораторных экспериментах при взрывах тонких проволочек сильным импульсом электрического тока [5, 6] и получившие название Z-пинчей. Природа их образования совершенно аналогична природе четочной молнии и разница только в масштабах явления. Аналогично происходит образование шаровых молний. Термином шаровая молния обозначают светящийся стабильный и сравнительно небольшой объект шарообразной формы, который наблюдается в атмосфере и возникновение которого связано с обычной молнией. Наблюдения шаровых молний показывают, что, как правило, их возникновение происходит в момент окончания разряда линейной молнии. Это зарегистрировано в экспериментах с инициированной молнией [4]. Этот факт говорит о том, что в отличии от четочной молнии образование шаровой молнии происходит за счет возбуждения замкнутой компоненты спирально-вихревой волны в ионизированном канале задним фронтом линейного разряда. Известны многочисленные явления образования долгоживущих сферообразных светящихся плазменных структур при искусственных электрических разрядах в различных средах [5, 6]. Анализ этих экспериментов показывает, что природа образования таких структур заключается в возбуждении мощным электрическим разрядом в ограниченном объеме ионизированной среды замкнутых спирально-вихревых волн. Другим примером существования в природе волновых спиронов служит атом, представляющий собой пример локального коллективного и самосогласованного движения электронов и ядра. В этом случае, из-за большой разницы масс и разных знаков зарядов электронов и ядра, электроны связаны с ядром, имеющим большую массу, кулоновскими силами и поэтому классическая компонента спиронной волны отсутствует, а существующая замкнутая спирально-вихревая компонента, в соответствии с уравнением (3), превращает электроны и ядро в замкнутую волновую динамическую систему. Кроме того, уравнение (3) аналогично по своей форме уравнению Клейна-Гордона, имеющему квантованные решения и применяющегося в квантовой и атомной физике. Различие этих двух уравнений заключается в виде пространственной частной производной второго порядка, которая в уравнении Клейна-Гордона имеет вид лапласиана определяющего, в общем случае, расширяющуюся сферическую волну, а в уравнении (3) эта производная имеет вид ротора от ротора и определяет замкнутую в пространстве волну. Второе отличие заключается в том, что коэффициент стационарного члена уравнения Клейна-Гордона представляет собой константу, а коэффициент стационарного члена в уравнении (3) представляет собой нелинейную скалярную функцию производных первого порядка по пространству и времени. Учитывая релятивистскую инвариантность уравнения (3) можно сделать вывод, что форма эмпирически полученного уравнения Клейна-Гордона является упрощенной линеаризованной формой уравнения (3). Примером, подтверждающим существование стационарных спиронов, может служить неустойчивость Бенара (конвективная неустойчивость) в жидких средах, во время которой, при критическом тепловом градиенте начинается макроскопическое движение среды и происходит четко упорядоченным образом с образованием цилиндрических или гексагональных стационарных структур – ячеек Бенара [7]. Такие стационарные структуры возникают в жидкой среде в соответствии с квазистационарным уравнением (5). Известны эксперименты с высокочастотным электромагнитным излучением, когда в разреженном газе или воздухе наблюдалось образование светящихся объектов «плазмоидов» напоминающих шаровую молнию [4, 10]. Их образование происходит в два этапа. На первом этапе в области пространства, где сфокусировано высокочастотное излучение большой интенсивности, происходит ионизация и пробой воздуха. На втором этапе в образовавшейся плазме начинают протекать спиронные волны плотности тока проводимости и в соответствии с уравнением (3) происходит образование волнового спирона. После выключения питания генератора высокочастотного излучения, волновой спирон продолжает существовать, пока не израсходуется свою энергию на поддержание ионизации плазмы и световое излучение. Условиями, стимулирующими и улучшающими образование спиронов, является повышение электропроводности среды. Это подтверждают эксперименты по образованию светящихся объектов при высоковольтном импульсном разряде в среде с примесью газообразного углеводорода (пропана) [4], при этом возникали объекты с меньшей энергией образования и имеющие большее время жизни. Это обусловлено меньшими затратами энергии на поддержание ионизации, для обеспечения необходимой проводимости среды. В астрофизике известно такое явление, как зернистость Солнечной фотосферы [11], это явление обусловлено возбуждением волновых спиронов в замкнутом объеме плазмы солнечной фотосферы. Таким образом, можно считать твёрдо установленным как теоретически, так и на основе наблюдения природных явлений и известных экспериментальных фактов существование свойства носителей заряда образовывать замкнутые нелинейные волновые и квазистационарные спирально-вихревые структуры - спироны, возникающие за счет взаимодействия носителей заряда с их самосогласованным электромагнитным полем. Открытие свойства носителей заряда образовывать спироны, затрагивает многие области физики и формирует единую теоретическую базу для объяснения физических явлений в таких областях, как физика плазмы, физика твёрдого тела, физика сверхпроводников, атомная физика, астрофизика, синергетика. Такой широкий круг затронутых областей связан с тем, что открытие относится к свойству носителей заряда, из которых состоит материальный мир. В работах [9, 10] приведён список особенно важных и интересных проблем физики нашего времени. Из тридцати перечисленных проблем это свойство носителей заряда, в той или иной степени, затрагивает десять (это 1, 2, 4-6, 11, 12, 24, 26, 29). Открытое свойство может найти применение при разработке новых методов удержания плазмы в виде спиронов, при создании лазеров, приборов твёрдотельной электроники, высокотемпературных сверхпроводящих материалов и в других областях использующих коллективные самосогласованные процессы носителей заряда.
ЛИТЕРАТУРА
- Спиричев Ю.А. Спиронные волны и спироны носителей заряда. www.sura.ru/SPIRON.
- Несис Е.И. Методы математической физики. М. 1977. 199 с.
- Спиричев Ю.А. Уравнения спирально-вихревых процессов в сплошных средах. www.sura.ru/SPIRON.
- Барри Дж. Шаровая и четочная молния. М., 1983, 288 с.
- Взрывающиеся проволочки. Сб. статей под ред. В.Г. Чейса и Г.К. Мура. М., 1981, 247 с.
- Быстрицкий Вит.М., Быстрицкий Вяч.М., Возняк Я. Дейтериевый лайнер и многопараметрическое исследование процесса формирование инверсного Z-пинча. ЖТФ, 2002, т. 72, вып.9, с. 29-37.
- Егоров А.И., Степанов С.И. Долгоживущие плазмоиды – аналоги шаровой молнии, возникающие во влажном воздухе. ЖТФ, 2002, т.72, вып. 12, с.102-104.
- Шабанов Г.Д. Оптические свойства долгоживущих светящихся образований. ПЖТФ, 2002, т. 28, вып. 4, с. 81-86.
- Хакен Г. Синергетика. М. 1980. 406 с.Бардош Л., Лебедев Ю.А. Электродный шаровой СВЧ разряд. Феноменология и результаты зондовых измерений. ЖТФ, 1998, т. 68, №12, с. 29-33.
- Смирнов Б.М. Введение в физику плазмы. М., 1982, 224 с.
- Гинзбург В.Л. Какие проблемы физики и астрофизики представляются сейчас особенно важными и интересными? УФН, 1999, т.169, №4, с. 419-441.
- Гинзбург В.Л. О некоторых успехах физики и астрофизики за последние три года. УФН, 2002, т.172, №2, с. 213-219.