ТЕОРИЯ И
КЛАССИФИКАЦИЯ
Главная страница
спиронные волны И СПИРОНЫ плотности тока проводимости
Spiron waves and spirons of current density conductivity
Из уравнений Максвелла и закона сохранения заряда получены уравнения нового типа волн плотности тока проводимости, распространяющихся в плазмоподобных средах. Особенностью этих волн является их отличие от классических волн описываемых волновым уравнением Даламбера и заключается в том, что они содержат замкнутую спирально-вихревую компоненту. Эти волны названы спиронными волнами плотности тока проводимости. Открытие спиронных волн объясняет причину неустойчивости плазмы, явление турбулентно-волнового динамо, зарождение турбулентности и спиральных автоволн в активных химических средах. Из уравнения спиронных волн следует, что в частном случае, когда отсутствует классическая компонента спиронной волны, может существовать ее замкнутая спирально-вихревая компонента, представляющая собой пространственно локализованный объект, образованный током проводимости. Эти локальные объекты названы спиронами плотности тока проводимости. Открытие спиронов плотности тока проводимости объясняет существование шаровых и четочных молний, искусственных долгоживущих плазменных образований, Z-пинчей.
Спиричев Ю.А.
Spirichev Yu.A.
E-mail: SPIRON@sura.ru
Дата 10.01.2003г.
Научно-информационный центр
спирально-вихревых процессов
и явлений "СПИРОН"
Существует ряд таких явлений, как многочисленные виды самопроизвольной неустойчивости и турбулентности плазмы, самозарождение турбулентности в жидких и газообразных средах, самовозбуждение плоских спиральных волн в активных средах плоских химических реакторов, многочисленные явления упорядочения и самоорганизации среды. Для объяснения этих явлений отсутствуют однозначные, взаимосвязанные физические теории и природа их образования остается неясной. В работе [1], на основании анализа тензора энергии-импульса электромагнитного и гидродинамического полей движущейся среды, делается вывод, что реакция материи на движение среды носит вихревой характер и является первопричиной возникновения гидродинамических вихрей, а также высказывается предположение, что турбулентность, как явление, выходит за рамки гидрогазодинамических понятий и является изначальным и всеобщим свойством физической материи в целом, и возможен единый подход к проблеме турбулентности. Анализ перечисленных явлений говорит о том, что все они имеют общую природу, связанную с коллективными самосогласованными движениями носителей заряда.
В соответствии с существующими представлениями в физике плазмы применяются два отличающихся друг от друга подхода, описывающие коллективные явления в плазмоподобных средах. В более простом, магнитогидродинамическом подходе среду рассматривают как нейтральную токопроводящую жидкость и для описания ее движения используют систему детерминированных уравнений магнитной гидродинамики [2-5]:
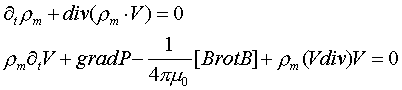
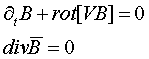
Здесь rm – массовая плотность проводящей жидкости;
V – скорость движения жидкости;
P – давление в жидкости;
В – магнитная индукция;
m0 – магнитная постоянная вакуума;
¶t – оператор частной производной по времени.
В магнитной гидродинамике не учитываются токи смещения и эта модель является квазистационарной. Существуют и другие разновидности гидродинамических моделей плазмоподобных сред (например, гидродинамика плазмы с анизотропным давлением Чи-Гольдбергера-Лоу), а также множество попыток их вывода, исходя из уравнений Больцмана, по аналогии с выводом уравнений обычной гидродинамики [3]. Известные системы уравнений магнитной гидродинамики имеют ограниченное применение для описания кинетики электропроводящих и плазмоподобных сред [5]. Другим, как считается, наиболее полным и строгим описанием кинетики носителей заряда, является уравнение с самосогласованным полем (уравнение Власова), основанное на описании среды как газа заряженных частиц. При этом подходе используют газокинетические законы, основанные на статистическом (вероятностном) описании распределения координат и скоростей заряженных частиц различных сортов. Модель такой среды представляет собой систему кинетических уравнений Власова для одночастичной функции распределения Fs для каждого сорта частиц s по импульсам Ls и пространству rs [3, 4]:
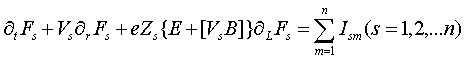 (1)
(1)
Здесь е – элементарный электрический заряд;
Zs – кратность заряда иона сорта s;
E – напряженность электрического поля;
B – магнитная индукция;
¶r и ¶L – операторы частных производных по r и L соответственно;
Ism – интеграл, учитывающий столкновения частиц сорта s и частиц сорта m.
Для нахождения внутренних самосогласованных с распределениями Fs электрических и магнитных полей, система кинетических уравнений дополняется уравнениями Максвелла, связывающими эти поля с плотностью токов проводимости J и объемной плотностью заряда r, в свою очередь определяемые через Fs [2, 4]:

Суммирование в этих выражениях распространяется по всем сортам s заряженных частиц среды. Введенные таким образом поля Е и В являются самосогласованными, поскольку из уравнения (1) получается такое распределение частиц Fs, которое вызывает появление электромагнитных полей, поддерживающих это распределение. Уравнение Власова является статистическим по своей основе, а входящие в него интегралы столкновений получены исходя из интеграла Больцмана и поэтому их решением, в отсутствии внешних сил, являются термодинамически равновесные распределения. Это подразумевает, что пространственные распределения плотностей и температур однородны, а среда нейтральна и температуры всех частиц равны между собой [5]. Отсюда следует, что и получаемые распределения самосогласованного электромагнитного поля, плотностей заряда и токов, также будут соответствовать термодинамически равновесным распределениям плотностей и температур.
В работе [5] отмечается, что самосогласованное взаимодействие описывает взаимодействие носителей заряда с электромагнитным полем, а интеграл столкновений – прямое, контактное взаимодействие частиц между собой. При этом взаимодействие носителей заряда посредством самосогласованного поля всегда больше, чем их прямое взаимодействие между собой. Из этого следует, что главным механизмом, определяющим самосогласованное движение носителей заряда, является электродинамическое взаимодействие на основе уравнений Максвелла, а не статистическое на основе уравнений Больцмана и Лиувилля.
Рассмотрим свободное самосогласованное движение носителей заряда в проводящей среде при отсутствии внешнего электромагнитного поля. При этом будем считать, что это движение носителей заряда первоначально возбуждается внешним электромагнитным полем. Из уравнений Максвелла известными способами получим обобщенное волновое уравнение [6]:
 (2)
(2)
Здесь e - относительная диэлектрическая проницаемость среды;
e0 – диэлектрическая постоянная вакуума;
m - относительная магнитная проницаемость среды;
m0 – магнитная постоянная вакуума;
с – скорость света в вакууме;
Δ – оператор Лапласа;
¶t, ¶tt – операторы частных производных первого и второго порядков по времени соответственно.
Левая, полевая часть уравнения (2) описывает электромагнитную волну, распространяющуюся в рассматриваемой области среды, а правая, материальная часть обычно рассматривается как возбуждающий эту волну источник, который представляет собой изменяющиеся во времени плотность тока проводимости и градиент плотности заряда. Но, справедливо и наоборот, рассматривать как возбуждающий источник, левую часть уравнения (2) и считать, что электромагнитная волна возбуждает в проводящей среде изменяющиеся во времени плотность тока проводимости и градиент плотности заряда (на этом принципе работают приемные радиоантенны). Для частного случая равенства нулю правой части уравнения (2)
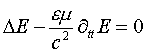 (3)
(3)
левая часть будет представлять собой классическое однородное волновое уравнение Даламбера (3) для напряженности электрического поля, имеющее наряду с тривиальными решениями Е=0 и нетривиальные решения Е¹0 и описывающее распространяющуюся электромагнитную волну, первоначально возбужденную изменяющимися плотностями тока проводимости и заряда, в соответствии с уравнением (2). Для этого частного случая, равная нулю правая часть уравнения (2)
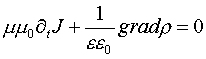 (4)
(4)
будет представлять собой однородное дифференциальное уравнение, имеющее тривиальные решения J=0 и r=0. Так как при движении носителей заряда выполняется закон сохранения заряда в виде уравнения непрерывности,
![]() (5)
(5)
то уравнения (4) и (5) необходимо рассматривать как систему связанных уравнений, которая будет описывать свободно изменяющиеся во времени плотности тока проводимости и заряда, первоначально вызванные воздействием электромагнитной волны на проводящую среду в соответствии с уравнением (2). Таким образом, кроме известных тривиальных решений правая часть имеет также и нетривиальные решения J¹0 и r¹0. Выполнив необходимые преобразования получим классическое скалярное однородное волновое уравнение Даламбера для плотности заряда
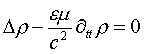 (6)
(6)
и векторное однородное волновое уравнение для плотности тока проводимости:
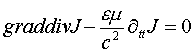 (7)
(7)
Уравнения (6) и (7) представляют собой систему волновых уравнений, описывающих свободные самосогласованные волны плотностей заряда и тока проводимости, первоначально возбужденные электромагнитной волной в соответствии с уравнением (2). Уравнение (6) для самосогласованной плотности заряда описывает продольные скалярные волны зарядовой плотности. Волны зарядовой плотности могут возбуждаться и распространяться в любых материальных средах: жидкостях, металлах, полупроводниках, диэлектриках. Образование этих волн в диэлектриках связано с эффектом поляризации, который также обусловлен перемещением в пространстве заряженных частиц, что равносильно протеканию в области, занятой диэлектриком, некоторых токов, называемых поляризационными. Векторное однородное, самосогласованное уравнение для плотности тока проводимости (7) имеет структуру классического векторного волнового уравнения Даламбера, но отличается от него видом своей «пространственной» частной производной второго порядка. В классическом векторном волновом уравнении Даламбера эта производная представляет собой лапласиан, который при точечном источнике, в случае фундаментального решения, определяет сферически симметричную волну, распространяющуюся от этого источника [8]. «Пространственную» частную производную второго порядка волнового уравнения (7), представляющую собой градиент дивергенции, можно представить, воспользовавшись известным векторным тождеством [9] в виде суммы лапласиана и оператора ротора от ротора плотности тока проводимости J
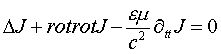 (8)
(8)
Волну плотности тока проводимости, описываемую уравнением (8), можно представить в виде суперпозиции двух волн:
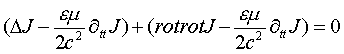 (9)
(9)
Первая компонента волны описывается классическим векторным уравнением Даламбера и для фундаментального решения представляет собой сферическую волну, распространяющуюся радиально от точечного источника. В соответствии с теоремой Стокса [7], поток ротора вектора через поверхность равен его циркуляции по замкнутому контуру на который опирается эта поверхность. Так как векторы rotJ и rotrotJ взаимно ортогональны, то “пространственная” часть второй компоненты волны, описываемой ротором от ротора вектора J, определяет циркуляцию вектора J по замкнутому спиральному контуру и соответственно описывает замкнутую спирально-вихревую волну вектора J. Для частного случая равенства нулю классической компоненты, замкнутая спирально-вихревая волна второй компоненты описывается уравнением:
 (10)
(10)
Таким образом, теоретически установлено, что из уравнений Максвелла и закона сохранения заряда следует существование в природе самосогласованных волн плотности тока проводимости, распространяющихся в виде особых волн, отличающихся от классических волн, описываемых уравнением Даламбера, наличием замкнутой спирально-вихревой компоненты. В соответствии с классификацией, приведенной в работе [10] волны плотности тока проводимости, описываемые уравнением (7) являются спиронными волнами плотности тока проводимости, а замкнутая спирально-вихревая компонента спиронной волны плотности тока проводимости, описываемая уравнением (10) является волновым спироном плотности тока проводимости. Спироные волны являются первопричиной зарождения турбулентности в плазме и других материальных средах, где есть свободные носители заряда. Наиболее наглядно существование спиронных волн проявляется в виде спиральных автоволн в химически активных средах. Поскольку во время протекания химической реакции происходит перемещение электронов и ионов, что эквивалентно протеканию токов, то это приводит к возбуждению спиронных волн, которые в плоских реакторах выглядят, как спиральные. Спироны плотности тока проводимости являются пространственно локализованными объектами. Их примерами могут служить четочные и шаровые молнии, искусственные долгоживущие плазменные образования, Z-пинчи. Спироны плотности тока проводимости образуются в случае невозможности распространения в пространстве классической компоненты спиронной волны из-за ограниченного объема области ионизации среды, например, канала разряда линейной молнии или Z-пинча. В этом случае спиронная волна вырождается в замкнутые локальные образования – спироны плотности тока проводимости. Открытие спиронных волн и спиронов плотности тока проводимости объясняет на единой теоретической основе большое число ранее не связанных между собой физических явлений и процессов.
Литература
1. Колмаков И.А. Электромагнитная природа возникновения турбулентности. М., ПЖТФ, 2002, т.28, вып.6, с. 81-86.
2. Смирнов Б.М. Введение в физику плазмы. М., 1982, 224 с.
3. Синкевич О.А., Стаханов И.П. Физика плазмы. Стационарные процессы в частично ионизированном газе. М., 1991, 191 с.
4. Франк-Каменецкий. Лекции по физике плазмы. М., 1968, 286 с.
5. Александров А.Ф., Рухадзе А.А. Лекции по электродинамике плазмоподобных сред. М., 1999, 336 с.
6. Гинзбург В.Л. Распространение электромагнитных волн в плазме. М., 1967, 684 с.
7. Несис Е.И. Методы математической физики. М. 1977. 199 с.
8. Владимиров В.С. Уравнения математической физики. М., 1981, 512 с.
9. Смирнов В.И. Курс высшей математики. Т.2. М., 1954, 627 с.
10. Спиричев Ю.А. Уравнения спирально-вихревых процессов в сплошных средах. www.sura.ru/SPIRON.