СПИРОНЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
Spirons of electromagnetic field
Из уравнений Максвелла и уравнения спирона плотности тока проводимости следует возможность существования в природе замкнутых волновых пространственно локализованных объектов, образованных электромагнитным полем. В этих объектах электромагнитная волна не распространяется в радиальном направлении, как классическая волна, описываемая уравнением Даламбера, а имеет замкнутый спирально-вихревой характер. Эти объекты названы спиронами электромагнитного поля. Источниками спиронов электромагнитного поля являются спироны плотности тока проводимости. Теоретическое открытие возможности существования в природе спиронов электромагнитного поля может позволить объяснить физику образования электронно-позитронных пар из квантов электромагнитного поля.
Спиричев Ю.А.
Spirichev Yu.A.
E-mail: SPIRON@sura.ru
Дата 10.01.2003г.
Научно-информационный центр
спирально-вихревых процессов
и явлений "СПИРОН"
В работе [1] приведено уравнение спиронных волн плотности тока проводимости:
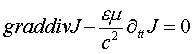
которое можно записать в виде уравнения, описывающего суперпозицию двух компонент спиронной волны плотности тока проводимости, классической и замкнутой спирально-вихревой компоненты
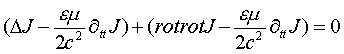 (1)
(1)
Для частного случая равенства нулю выражения, описывающего классическую компоненту спиронной волны
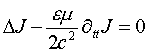 (2)
(2)
возможно самостоятельное существование в природе замкнутой спирально-вихревой компоненты спиронной волны плотности тока проводимости:
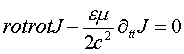 (3)
(3)
В соответствии с классификацией приведенной в работе [2], эта компонента является пространственно локализованным объектом, образованным током проводимости – волновым спироном плотности тока проводимости. Из первого уравнения Максвелла следует выражение для плотности тока проводимости через магнитную индукцию и напряженность электрического поля:
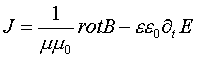
Подставив это выражение для плотности тока в уравнение (3) получим следующее уравнение:
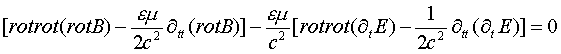
Это уравнение представляет собой описание суперпозиции замкнутой спирально-вихревой волны ротора магнитной индукции и замкнутой спирально-вихревой волны тока смещения. В соответствии с теоремой Стокса, поток ротора вектора через поверхность равен его циркуляции по замкнутому контуру на которую опирается эта поверхность, а так как векторы rot(¶tЕ), rot(rotВ) и rotrot(¶tЕ), rotrot(rotВ) ортогональны то, следовательно, “пространственные” части компонент этой электромагнитной волны, описываемой ротором от ротора векторов ¶tЕ и rotВ, определяют циркуляцию этих векторов по замкнутым спиральным контурам. Отсюда следует, электромагнитная волна, описываемых уравнением (4) представляет собой замкнутое локальное волновое спирально-вихревое образование электромагнитного поля или волновой спирон электромагнитного поля. Поскольку это волновое образование является замкнутым, то оно не распространяется в пространстве, как обычная волна, а после своего возбуждения остается локализованным пространственным электромагнитным объектом. В работе [3] по результатам наблюдений за электрическими атмосферными явлениями высказывается предположение о возможности существования в природе электрометеоров, что подтверждается уравнением (4). В радиолокации известны аналогичные объекты, получившие название «ангелов». Известно, что кванты электромагнитного поля могут образовывать пары электрон - позитрон и мюон - антимюон. До настоящего времени отсутствует теория внутренней структуры этих частиц. Уравнение (4) можно привести к виду
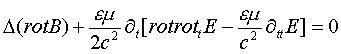
D(rotB) говорит о наличии магнитного момента, а наличие магнитного момента говорит о существовании механического момента. Из квантовой механики известно [4], что оператор rot представляет собой произведение операторов спина и импульса, что подтверждает существование у спиронов, описываемых уравнением (5) существование механического момента (спина). Уравнение (5) несложно привести к виду graddivE=F(xyz), где F(xyz) произвольная, не зависящая от времени функция. При этом с учетом размерности можно положить F(xyz)=gradr/ee0. Тогда уравнение (5) приводиться к виду divE=r/ee0, а это означает, что спироны электромагнитного поля обладают зарядом. Наличие коэффициента 1/2 у второго члена может указывать на кратность спина электронов и мюонов. Таким образом можно предположить, что спироны электромагнитного поля, описываемые уравнением (4), являются классическим описанием структуры электронов и мюонов.
ЛИТЕРАТУРА
1. Спиричев Ю.А. Спиронные волны и спироны плотности тока проводимости. www.sura.ru/SPIRON
2. Спиричев Ю.А. Уравнения спирально-вихревых процессов в сплошных средах. www.sura.ru/SPIRON
3. Александров М.С. Исследование атмосферных радиопомех ОНЧ- и НЧ-диапазонов и их источников. Успехи современной радиоэлектроники. 1998, №10, с.3-25.
4. Мессиа А. Квантовая механика. Т.2, М., 1979, 584 с.